異常検知ビジネスで活用できる外れ値検知手法まとめ
機械学習の中でも教師なし学習に分類される分野として異常検知という技術があります。研究分野としては近年下火になりつつあるものの、人工知能やAIを使った異常検知技術はビジネス界隈では期待の大きい分野として有名です。
本記事では、異常検知分野のなかでも外れ値検知の一般的な手法についてまとめました。
目次
はじめに
外れ値検知はビジネスにおけるさまざまな場面で使用されています。
外れ値検知とは、正常時の状態から外れた点を見つけ出す異常検知の種類のひとつです。クレジットカードの利用状況の解析などでは、異常な行動を即時に検出することで被害の拡大を防ぐことができます。また、工場などのモニタリングでは、機械の異常状態をセンサなどで検知してアラートを出すなどのユースケースが考えられます。大量のデータをモニタリングする必要のあるセキュリティ分野や機械などを無人でモニタリングするスマートファクトリー分野のほか、高齢者の転倒検知や患者の体調急変といった予測に需要があるヘルスケア分野などでも実用化が始まっています。
それでは、最初におさえておきたい4つの基本的な外れ値検知手法について確認していきます。
ホテリング理論
最も基本的な手法として、ホテリング理論による外れ値検知について紹介します。
この手法は平均や分散といったデータの基本的な分布情報をもとに、観測値 x' より算出した異常度 a(x') を用いて外れ値検知を行うものです。まずは一般的な外れ値手法を理解するところから始めましょう。
はじめに、ほとんど外れ値が含まれていない1次元のデータセットを用意します。ホテリング理論ではこのデータセットが正規分布に従うことを大前提としているため、ヒストグラムやQQ Plot などを使って正規分布であることを確認しておきましょう。もし正規分布でない場合は対数変換やボックスコックス変換などをかけて正規化する必要があります。
正規分布を仮定した場合、ホテリング理論をもとに算出した異常度はデータ数が十分に大きければ自由度1のカイ二乗分布に従うとされています。

異常発生の確率値 α を定義すれば、カイ二乗分布の表から異常度の閾値を求めてることができます。たとえば、発生確率が 1% 以下のものを異常値とするのであれば、α = 0.01 に対応する異常度を閾値に設定すればよいということになります。
異常度は次式で求めることができます。
以上が1次元データにおけるホテリング理論による外れ値検知でした。
多次元データ(2次元以上)にこれを適用する場合は、マハラノビス距離という指標を異常度として採用します。マハラノビス距離とは、データの分布を考慮した距離の指標です。
1次元データでは平均と分散を求めましたが、多次元データでは標本平均と標本共分散行列を下記のように求めます。
また、異常度はマハラノビス距離を用いて以下のように求めることができます。
1次元でも多次元でも、異常度というスカラー値に落としこんでいるという点では共通していることがわかります。このように求めた異常度に閾値を設定することで、異常か正常かを識別することができます。
明らかに分布から外れている異常点を検出したいときには有効な手法です。
k-近傍法 (k-NN)
あまり有名ではないものの、シンプルに実装ができる古典的な手法として k-近傍法 (k-NN) による外れ値検知 があります。k-近傍法は k-nearest neighbor 法とも呼ばれていますが、異常検知におけるk-近傍法は機械学習の最も基本的な分類手法である k-NNとは少し異なることに注意してください。
想像ができている方もいらっしゃると思いますが、この手法ではk-NNと同様にある点から最も近い k 個の点を考慮して外れ値検知を行います。対象の点から近傍のk個の点を含むような円を描きます。
次の例では k=5 のときを考えます。
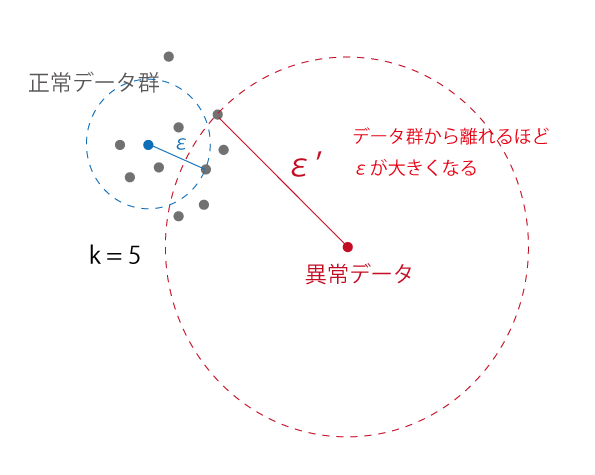
このとき、データ群から離れた異常点が描く円の半径 ε は正常データ群のものよりも大きくなっていることがわかります。
この性質に基づき、ε を異常度として使用して外れ値検知を行います。具体的には、εがある閾値を超えた場合は異常、そうでない場合は正常といったようにスカラー値に落として外れ値を検出することができます。
メリットとして、多次元データにもそのまま適用できるということがあります (ただし、次元数が10以下を目安と考えたほうがよいでしょう)。一方で、すべての点との距離を計算する必要があることから、計算量が大きくなってしまうというデメリットがあります。
Local Outlier Factor (LOF)
同じく距離をベースにした外れ値検知手法として、Local Outlier Factor (LOF) を紹介します。
この手法では 局所密度 (Local density) という指標に注目します。 局所密度は、周辺の点との密度を表します。点Aは近傍の点 B, C, D との距離が大きいため、局所密度が低いということになります。一方で、点B, C, D はそれぞれの近傍点との距離が近いため局所密度が高いといえます。

つまり、近傍点の局所密度が類似している場合には近くにデータが集まっているということがわかります。点Aのようにデータ群と離れているような点の場合、自身の局所密度と近傍点の局所密度の差が大きいということになります。この差を利用して外れ値を検出することができるのが LOF です。
より詳しい内容については次の記事でまとめたので興味がある方はご確認ください。
One class SVM (Support Vector Machine)
分類アルゴリズムである Support Vector Machine (SVM) を応用した外れ値検知手法として、One class SVM を紹介します。
One class SVMとは、機械学習の分類アルゴリズムである Support Vector Machine (SVM) を教師なしの1クラスに適用した手法です。正常データとして1つのクラス分を学習させ、識別境界を決定することで、その境界を基準として外れ値を検出します。異常がほとんど発生せず、異常クラスのデータを集めにくいようなシステムで異常検知を実現したい場合には有効な外れ値検知手法です。
One class SVMではすべての学習データをクラスタ 1とし、原点のみをクラスタ -1に属するようにカーネルトリックと呼ばれる手法を用いて、高次元空間の特徴空間へデータを写像します。このとき、学習データは原点から遠くに配置されるように写像されるため、もとの学習データと類似していないデータは原点の近くに集まるようになります。

One class SVM のメリットとしては、学習したデータをもとに複雑な境界線を引くことができるという点があります。一方で、パラメータをチューニングする必要があるというデメリットもあります。
One class SVM については次の記事でより詳細にまとめています。
hktech.hatenablog.com
まとめ
異常検知ビジネスで活用できる一般的な外れ値検知手法についてまとめました。外れ値検知をサービスや研究などで使おうと考えている方には参考になる内容になっているかと思います。Deep Learning などを使ってなにかを始めようとする前に、まずはこの記事で紹介されているような基本的なアルゴリズムで試してみてはいかがでしょうか。
